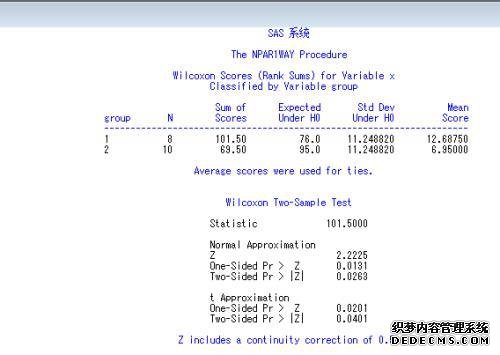
以提高结果的准确性。
对于任意全局分布,已经发现成对的测试数据的分布位置明显不同,并且通常可以通过符号验证来实现。
但是,因为符号测试仅考虑差异的符号,所以不管差异的绝对值有无差异,都会丢失一些测试信息,并且结果是相对近似的。
为了避免符号验证方法中的这种缺陷,Wilcoxon提出了一种改进的方法,称为Wilcoxon秩和检验。
该方法考虑了差异的方向和差异的大小。这比符号测试更有效。
该组的一般测试数据的分布没有差异,可以使用类似的方法进行测试。
使用扩展的数据来比较两个连续总体的中位数非参数假设检验。
令X和L为两个连续的总体。H0:为了检验X和y相等的零假设,分别提取X和y的简单随机样本(Xl,...,X)。
并且(y1,...,y0),因为这两个样本是根据其观测值混合而成,并从最小值到最大值进行组织,所以Ri是这些数字l + n2的yi的范围(即,首先是yi这是一个规则)。
小),则这些范围的总和为Wy = ∑R,并且在建立零假设时,WY = 1应该太小或太大。
因此,WY可以用作检查两个总体的中位数是否相同的基础。
资料来源:百度百科-威克森排名和测试资料来源:百度百科-范围和测试